Hipoteza Riemanna
Dziś zajmiemy się jednym z nierozwiązanych Problemów Milenijnych, za które jest nagroda równa 1mln $.
Zaczniemy od przedstawienia wzory na funkcję dzeta.
A wygląda ona tak:
Funkcja ta daje się jednoznacznie przedłużyć analitycznie na całą płaszczyznę zespoloną, nie licząc punktu
Ogólnie funkcję zeta Riemanna możemy zapisać w poniższy sposób:
Dla mamy
Z powyższego wyrażenia wyniki, że funkcja jest holomorficzna co oznacza, że funkcja zdefiniowana na otwartym podzbiorze płaszczyzny liczb zespolonych
o wartościach w
która jest różniczkowalna w sensie zespolonym w każdym punkcie tego podzbioru.
Euler wykazał, że , gdzie
oznacza zbiór liczb pierwszych.
Wynika również następująca tożsamość:
dla
Wiemy, że już w starożytności udowodniono, że liczb pierwszych jest nieskończenie wiele (sito Eratostenesa).
Z kolei Gauss badał tabele liczb pierwszych i doszedł do wyrażenia:
. Wynia z tego, że:
Pomocne było wynalezienie logarytmu całkowego, który prezentuje się tak:(zapisujemy go tam, jeśli rozważamy go w teorii liczb)
z czego obserwujemy, że:
przy
Przy zerze dążącym do nieskończoności błąd będzie malał (wg twierdzenia o liczbach pierwszych).
Teraz o samej hipotezie Riemanna, która brzmi:
Część rzeczywista każdego nietrywialnego zera funkcji równa się
.
Wynika z tego, że wszystkie nietrywialne zera funkcji leżą na prostej krytycznej równej:
dla
Z racji, że możemy się jednoznacznie przedłużyć analitycznie funkcję zeta to przyjmuje ona postać równania funkcyjnego:
gdzie:
to funkcja gamma, która już omawialiśmy na blogu.
Pisząc o hipotezie Riemanna warto wspomnieć o notacji dużego O.
Na początek zdefiniujmy duże O:
Funkcja X jest równa O duże od funkcji Y, jeśli dla wystarczająco dużych argumentów wartości funkcji X nigdy nie przekraczają pewnej określonej krotności wartości funkcji Y.
Hipoteza Riemanna jest równoważna poniższej równości:
gdzie
oznacza resztę z logarytmu całkowego.
Przy hipotezie Riemanna rozważa się tzn funkcję Möbiusa:
jeśli liczba n jest podzielna przez kwadrat liczby pierwszej,
jeżeli liczba
jest iloczynem
różnych liczb pierwszych.
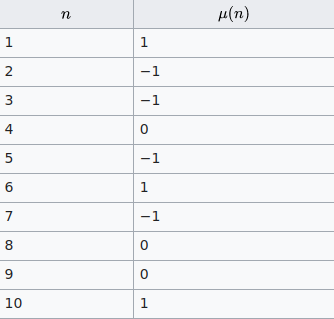
Poniżej wartości funkcji dla małych n. Gdy n jest liczbą pierwszą wartość funkcji wynosi -1.
Filed under: Teoria liczb - @ 5 grudnia 2021 07:20
Tagi: hipoteza riemanna, liczby pierwsze, logarytm całkowy, matematyka
Hipoteza Riemanna już dziś jest stosowana przy znajdowaniu liczb pierwszych, które są wykorzystywane m.in. w algorytmach kryptograficznych. Miejsca zerowe funkcji dzeta mają też interpretację fizyczną – ich rozkład odpowiada rozkładowi poziomów energetycznych w atomach pierwiastków ciężkich.