Powierzchnie jednostronne
Dziś krótki artykuł o powierzchniach jednostronnych.
Na początek: czym taka powierzchnia się charakteryzuje?
Najprościej mówiąc to taka powierzchnia, którą całą możemy pokolorować bez odrywania od niej ołówka, tak by, nie “przejść” przez brzeg powierzchni.
Dziś jako przykład takich powierzchni podam wstęgę Möbiusa oraz butelkę Kleina.
Zaczniemy od wstęgi Möbiusa.
Groźnie to zabrzmi ale ta wstęga to: dwuwymiarowa zwarta rozmaitość topologiczna istniejąca w przestrzeni trójwymiarowej.
Spróbuję przybliżyć to pojęcie na przykładzie właśnie tej wstęgi.
Aby ona powstała wystarczy skleić dwa końce prostokątnej wycinki, skręcając jeden koniec o kąt 180°.
Najlepiej będzie pokazać tę powierzchnię na obrazku:

Teraz sami możecie sprawdzić, że tak sklejoną powierzchnię, można pokolorować w całości, bez odrywania ręki od niej.
Jedną z własności owej wstęgi jest możliwość “sklejenia” jej krawędzi (ma ją ona tylko jedną) tak by powstała butelka Kleina. Jest to niemożliwe do wykonania w przestrzeni trójwymiarowej.
A więc teraz słowo o butelce Kleina.
Jest to także powierzchnia jednostronna. Najprościej mówiąc jest to prostokąt, w którym “sklejono” parami odpowiednie punkty przeciwległych boków, ale jedna para została przed sklejeniem, obrócona o kąt 180°.
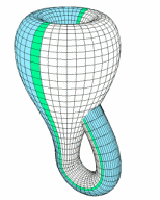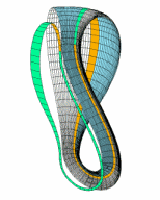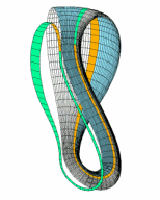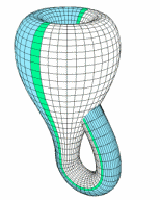
Tak wygląda butelka Kleina w przestrzeni trójwymiarowej:

Jak pisałem wcześniej butelkę Kleina można skonstruować z wstęgi Möbiusa.
Aby to zrobić należy skleić wszystkie punkty brzegu wstęgi. Można także skleić dwie wstęgi brzegami.
Na koniec ciekawostka: Butelka taka istnieje bez przecięć w przestrzeni czterowymiarowej ale już nie w trójwymiarowej, gdzie powstałyby samoprzecięcia.
I na koniec gif przedstawiający butelkę Kleina konstruowaną z dwóch wstęg Möbiusa:
Filed under: Topologia - @ 29 października 2014 12:35
Tagi: butelka, butelka Kleina, Klein, Möbius, topologia, wstęga, wstęga Möbiusa